Question

Matt wants to build a rectangular enclosure for this animal. One wide of the pen will against the barn. So he needs no fence on that side. The other three sides will be enclosure with wire fencing. If Matt has 1000 feet of fencing. You can find the dimensions that maximizes the area of the enclosure.

Answer 1

A = 90,312.5 square feet is the maximum area.

Explanation:

Here, the shape of the enclosure = Rectangle

Now, 3 sides of the rectangle needs to be fenced.

Total length of the fencing wire = 1000 ft

Let us assume the length of the enclosure = L

The width of the enclose = W

According to question:

The length to fenced = Perimeter of the rectangle - 1 side of Enclosure

⇒ 1000 = 2 (L + W) - L

or, 1000 = L + 2 W

or, L = 1000 - 2 W .... (1)

Now, as we need to MAXIMIZE the area of the enclosure:

Area of the enclosure = L x W = (1000 - 2 W) x W

Now simplifying the area expression, we get:

`A(w) = 1000 w - 2w^2`

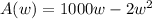
This is a parabola that opens downward so there is a maximum point.

The vertex of the parabola is (h,k) where h is the "maximizing number" and k is the maximum area.

Use the fact that h = -b/2 a

h = -850/(2*[-2])

h = -850/(-4)

h = 212.5 would be the length of all four sides if it were not for the barn

Therefore you have an extra 212.5 feet

Add the 212.5 feet to the opposite side(length) to get 425 feet.

You have a rectangle that is 212.5 feet by 425 feet by 212.5 feet by "the barn".

The width is 212.5 feet which maximizes the area.

A = l w

A = 425*212.5

A = 90,312.5 square feet is the maximum area.