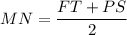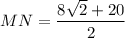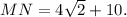Answer:

Explanation:
Given:
FPST is a trapezoid,
FP=ST, m∠F=45°,
PF=8, PS=10
To Find:
The Length of the mid-segment MN.
Solution:
This trapezoid FPST is isosceles, because FP=ST
Also
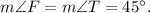
Draw the height PH. Triangle FPH is right triangle with two angles of measure 45°. This means that
FH = HP --------------(1)
By the Pythagorean theorem,

From (1)
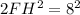



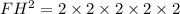

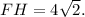
Since trapezoid FPST is isosceles, the base FT has the length
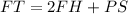

Then the length of the mid-segment is