Question

Find the amount necessary to fund the given with drawls. Quarterly withdrawals of $850 for 9 years with an interest rate of 4.4% compounded quarterly

Answer 1

The principal amount necessary to fund is $573.31

Explanation:

Given as :

The quarterly withdrawal amount = A = $850

The time period for withdrawals = t = 9 years

The rate of interest = r = 4.4% compounded quarterly

Let The principal amount necessary to fund = $p

Now, From Compound Interest

Amount = Principal ×
`(1+(rate)/(100* 4))^(4* time)`

Or, $850 = p ×
`(1+(r)/(100* 4))^(4* t)`

Or, $850 = p ×
`(1+(4.4)/(100* 4))^(4* 9)`

Or, $850 = p ×
`(1.011)^(36)`

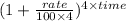
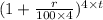
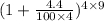
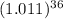
Or, $850 = p × 1.4826

∴ p =
`(850)/(1.4826)`

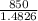
i.e p = $573.31

So,The principal amount necessary to fund = p = $573.31

Hence, The principal amount necessary to fund is $573.31 Answer