Question:
A ball is thrown into the air with an initial velocity of 22 meters per second.
The quadratic function h(t) = -4.9t2 + 22t + 5.5 represents the height of
the ball above the ground, in meters, with respect to time t, in seconds.
Determine h(3) and explain what it represents.
Answer:
h(3) = 27.4
h(3) = 27.4 means that the ball throw into the air with an initial velocity of 22 meters per second is 27.4 meters above the ground after 3 seconds.
Solution:
The quadratic equation that represents the height of the ball above the ground, h(t), in meters, with respect to time, t, in seconds is given by:

To find h(3), substitute t = 3 into given quadratic equation and solve for it
Plug in t = 3 in h(t)
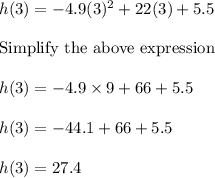
Thus h(3) = 27.4
h(3) = 27.4 means that the ball throw into the air with an initial velocity of 22 meters per second is 27.4 meters above the ground after 3 seconds.