Question

How do you write a compound inequality

Answer 1

Compound inequality:

A compound inequality contains two or more inequalities that are separated either by "and" or "or".

And: It indicates that both statements of the compound sentence satisfies at the same time.

Or: This indicates that as long as either statement is true, the entire compound sentence is true.

For example:

1.
`3 x + 2 < 14 \text{ and }2 x-5 >-11`

Here, and denotes that intersection or the overlap will be the desired result.

2.
`2 x + 7 <-11 \text{ or }-3 x-2 < 13`

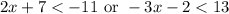
Since the joining conjunction is or we can come to a point that the entire compound sentence is true.

AND CASES:

A number is a solution to the compound inequality if the number is a solution to both inequalities. It can either be written as x > -1 and x < 1 or as -1 < x < 1.

OR CASES:

A number is a solution to the compound inequality if the number is a solution to at least one of the inequalities. It is written as x < -1 or x > 1.