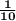Question

what is the probability that a randomly selected two digit positive integer will be a multiple of 11 ? express your answer as a common fraction.

Answer 1

The probability that a randomly selected two digit positive integer will be a multiple of 11 is
`\bold{(1)/(10)}`

Solution:

Number of sample space n(S):

Total number of two digit positive integers = 90

Favorable event P(A):

Two digit multiples of 11 =
`\bold{(11, 22, 33, 44, 55, 66, 77, 88, 99)}`

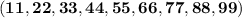
Number of favorable outcome n(A):

Total number of two digit multiples of 11 = 9

Let us consider the requires probability as P(A); number of favorable outcomes as n(A) and the number of sample space as n(S).

The probability formula is as follows,

`$P(A)=\frac{\text { n(A)}}{\text { n(S) }}`

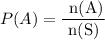
On substituting the values in the above formula we get,

`$\Rightarrow P(A)=(9)/(90)`

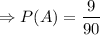
On simplifying the above equation we get,

`$\Rightarrow P(A)=(1)/(10)`

The required probability is
`\bold{(1)/(10)}`