Question

The square of the sum of two numbers is 144 and the sum of of their square is 180, find the number... Please I really need the answer now ​

Answer 1

The numbers are either ±13.35 and ±1.35 or ±1.35 and ±13.3

Explanation:

Let the two numbers be 'x' and 'y'.

Given:

The squares of the sum of two numbers = 144

The sum of their squares = 180

The sum of the numbers =
`x+y`

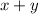
The square of the sum of numbers =
`(x+y)^2`

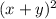
Square of first number =
`x^2`

Square of second number =
`y^2`

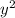
The sum of their squares =
`x^2+y^2`

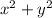
Now, as per question:

`(x+y)^2=144---(1)\\\\x^2+y^2=180---(2)`

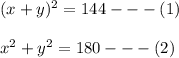
Expanding equation (1) using the formula
`(a+b)^2=a^2+b^2+2ab`

This gives,

`(x+y)^2=144\\\\x^2+y^2+2xy=144\\\\\textrm{Plug in the value of }x^2+y^2\textrm{ from equation (2)}\\\\180+2xy=144\\\\2xy=144-180\\\\2xy=-36\\\\xy=-(36)/(2)\\\\xy=-18\\\\y=-(18)/(x)---(3)`

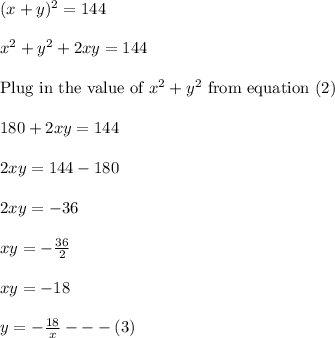
Plug in the value of 'y' from equation (3) in equation (1). This gives,

`x^2+(-(18)/(x))^2=180\\\\x^2+(324)/(x^2)=180\\\\x^4+324=180x^2\\\\x^4-180x^2+324=0\\\\\textrm{On solving, we get:}\\\\x^2=178.2\ or\ x^2=1.8\\\\\textrm{Square root both sides, we get:}\\\\x=\pm13.35\ or\ x=\pm1.35`

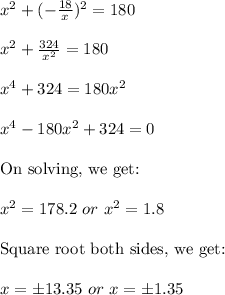
Therefore,

`y=-(18)/(x)=-(18)/(\pm13.35) = \pm1.35\ or\\\\y=-(18)/(x)=-(18)/(\pm1.35)=\pm13.3`

Therefore, the numbers are either ±13.35 and ±1.35 or ±1.35 and ±13.3