Question

Lamont works for an electric utility and is installing a 40 foot utility pole as shown. Lamont drills the anchor of a support cable into the ground 15 feet from the base of the pole. What is the minimum length of cable Lamont needs?

Answer 1

Approximately 43 feet of minimum cable is needed.

Explanation:

This problem can be solved using Trigonometry and Pythagorean theorem. Pythagorean theorem applies on right-triangles (which are known to have one 90° angle). The theorem states that the square of the Hypotenuse is obtained by the squared sum of the other two sides of the triangle (i.e the two sides forming the 90° angle - with the hypotenuse side being across it as:

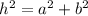`h^2=a^2+b^2` Eqn. (1)

where

`h` is the hypotenuse

`a` is a side

`b` is a side

Now in this case, the utility pole must be perpendicular to the ground and the anchor being parallel to the ground, and a 90° angle formed between them. Conclusively the cable length will be represented by the hypotenuse in a right triangle. So here we have
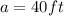`a=40ft` and
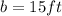`b=15ft`. Plugging in Eqn.(1) and solving for
`h` we have:

`h^2=40^2+15^2\\h=√(40^2+15^2) \\h=√(1600+225)\\ h=√(1825)\\ h=5√(73)\\ h=42.72ft`

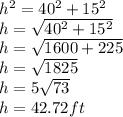
So we conclude that the minimum length of cable needed by Lamont is

≈43 feet (rounded up).