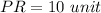Answer:
Therefore,
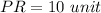
Explanation:
Given:
PR = 2x
RQ = 25
Say M divide PQ such that
PM = 6
MQ = 3x
∠PRM ≅ ∠QRM
RM is the angle Bisector of angle PRQ
To Find:
PR = ?
Solution:
Angle Bisector Theorem:
The angle bisector theorem is concerned with the relative lengths of the two segments that a triangle's side is divided into by a line that bisects the opposite angle.
It equates their relative lengths to the relative lengths of the other two sides of the triangle.
Here RM is the angle Bisector of angle PRQ
Therefore,
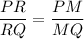 ...Angle Bisector Theorem.
...Angle Bisector Theorem.
Substituting the values we get
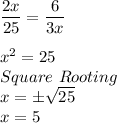
As x cannot be negative x =5
Substituting x value in PR we get
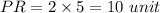
Therefore,