Question

The square of the sum of two numbers is 144 and the sum of their square is 180, find the numbers ​

Answer 1

x = 13.35, y = - 1.35

or, x = 1.35, y = - 13.35

or, x = - 13.35, y = 1.35

Explanation:

Let us assume that x and y are the two numbers.

So, given that (x + y)² = 144

⇒ x² + 2xy + y² = 144 ........ (1)

⇒ x + y = ± 12 ......... (2)

Again, x² + y² = 180 ........... (3)

Now, from equations (1) and (3) we can write 2xy + 180 = 144

⇒ 2xy = - 36

⇒ xy = - 18 ........ (4)

Now, for x + y = 12

⇒
`x - (18)/(x) = 12`

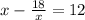
⇒ x² - 18 = 12x

⇒ x² - 12x - 18 = 0

Using the quadratic formula

`x = \frac{12 \pm \sqrt{(-12)^(2) - 4(1)(-18) } }{2}`

⇒
`x = (12 \pm 14.7)/(2) = 13.35, 1.35`

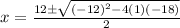
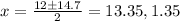
Now, for x = 13.35, from equation (4) we get, y = - 1.35

And for x = 1.35, from equation (4) we get, y = - 13.35

Now, for x + y = - 12

⇒ x² + 12x - 18 = 0

Using the quadratic formula,

`x = \frac{- 12 \pm \sqrt{12^(2) - 4(1)(-18)}}{2}`

⇒
`x = (- 12 \pm 14.7)/(2) = 1.34, -13.35`

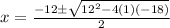
Now, for x = - 13.35, from equation (4) we get, y = 1.35

And for x = 1.35, from equation (4) we get, y = - 13.35

Therefore, x = 13.35, y = - 1.35

or, x = 1.35, y = - 13.35

or, x = - 13.35, y = 1.35 (Answer)