Question

A ball is throw into the air from the top of a building. The height h(t) of the ball above the ground t seconds after it is thrown can be modeled by h (t) =-16t +64t+80 how many seconds after being thrown will the ball hit the ground

Answer 1

Answer: The ball will hit the ground 5 seconds after being thrown.

Explanation:

The correct function is:
`h (t) =-16t^2 +64t+80`

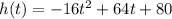
You can rewrite the Quadratic function given in the exercise with making
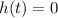`h(t)=0`. Then this is:

`0=-16t^2 +64t+80`

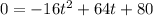
Now you can simplify the equation dividing both sides by -16. So you get:

`(0)/(-16)=(-16t^2 +64t+80)/(-16)\\\\0=t^2-4t-5`

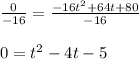
To find the solution of the Quadratic equation, you can facfor it. In order to do this, it is necessary to find two numbers whose sum is -4 and whose product is -5. These number would be -5 and 1.

Therefore, you get this result:

`0=(t-5)(t+1)\\\\t_1=5\\t_2=-1`

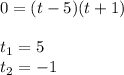
Since the time cannot be negative, you can conclude that the ball will hit the ground 5 seconds after being thrown.