Answer:
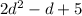
Explanation:
The total number of burgers sold from a restaurant from Monday to Sunday:
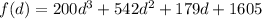
The number of visitors to the restaurant from Monday to Sunday:
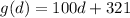
To find the average number of burgers per person, just divide
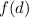 by
by
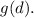
First, multiply
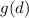 by
by
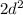 and subtract the result from
and subtract the result from
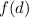 :
:
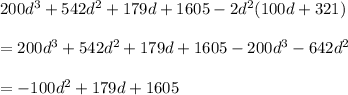
Then, multiply
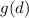 by
by
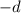 and subtract the result from
and subtract the result from
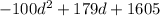 :
:
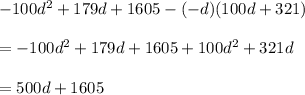
Now, multiply
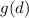 by
by
 and subtract the result from
and subtract the result from
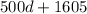 :
:
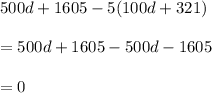
Hence,
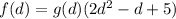
and the function
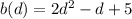
represents the average number of burgers per person.