Question

A plane is flying east at 115 m/s. The wind accelerates it at 2.88 m/s^2 directly northwest. After 25.0 s, what is the direction of the velocity of the plane?

Answer 1

Answer: 38.5 degrees

======================================================

Step-by-step explanation:

The east direction is the vector < 1, 0 >

If the plane is flying in this direction, we want a vector to point in the direction of < 1, 0 > and we want it to have a magnitude of r = 115. So we simply scale this vector with scale factor 115

< 1, 0 > turns into < 115, 0 >

I multiplied both coordinates by 115.

If we do not account for the wind, the plane's velocity vector is
`< 115, 0 >`

--------------------------------------------

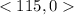
The wind's velocity vector is a bit trickier. We're told that the magnitude of the wind's acceleration vector is 2.88 m/s^2. This means every second, the wind's speed is increasing by 2.88 m/s. After 25 seconds, the speed of the wind is 25*2.88 = 72 m/s, which is the magnitude of the wind vector.

So r = 72

The angle of the wind is theta = 135 as we are in the northwest direction, so we subtract 45 from 180 getting 180-45 = 135. The diagram below might help. The purple vector is in quadrant Q2. Alternatively, you can add 45 degrees to 90 and you'd get 45+90 = 135 which is the same direction.

The x and y components of the wind's velocity vector is

x = r*cos(theta) = 72*cos(135) = -50.911688 = -50.9

y = r*sin(theta) = 72*sin(135) = 50.911688 = 50.9

meaning that

`< x, y > = < -50.9, 50.9>`

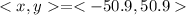
is the approximate wind velocity vector

-----------------------------------------------------

What do we do from here? Well we have the plane's velocity vector
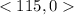`< 115, 0 >` , without the wind involved, and we have the wind's vector of
`< -50.9, 50.9>`

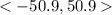
Vector addition will yield the resultant vector. This vector is the true direction of where the plane is going after we account for the wind speed. Without the wind speed, the plane will go directly east. However, with the wind speed, the plane will go in the direction of the red vector arrow (see diagram below).

So we have,

`< 115, 0 > + <-50.9, 50.9> = <115+(-50.9), 50.9>`

`<115, 0> + <-50.9,50.9>= < 64.1, 50.9>`

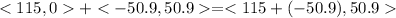
The plane's resultant vector is approximately
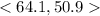`<64.1, 50.9>` which is the velocity vector of the plane after we account for wind.

-----------------------------------------------------

The last step is to compute the theta of this resultant vector

theta = arctan(b/a)

theta = arctan(50.9/64.1)

theta = 38.452096

theta = 38.5

This theta value is represented of the red vector in the diagram below.