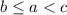Answer: C) 30, 40, 50
=========================================
Step-by-step explanation:
Use the pythagorean theorem to determine if we have a right triangle or not.
Choice A is not a right triangle because
a^2+b^2 = c^2
2^2+3^2 = 4^2
4+9 = 16
13 = 16
is false. So a triangle with sides a = 2, b = 3, c = 4 is not a right triangle
-----------
The same applies to choice B as well
a = 10, b = 20, c = 30
a^2+b^2 = c^2
10^2 + 20^2 = 30^2
100+400 = 900
500 = 900 is false
Cross choice B off the list.
-----------
Choice C is true however
a = 30, b = 40, c = 50
a^2 + b^2 = c^2
30^2 + 40^2 = 50^2
900 + 1600 = 2500
2500 = 2500 is true
So a triangle with sides 30, 40, 50 is a right triangle.
It is based off the 3,4,5 right triangle (multiply all three sides by 10 to scale it up).
-----------
For the sake of completeness, let's check choice D.
a = 4, b = 5, c = 6
a^2 + b^2 = c^2
4^2 + 5^2 = 6^2
16 + 25 = 36
41 = 36 is false
So a triangle with sides 4,5,6 is not a right triangle.
-----------
Note: for each answer choice, the longest side is always c. The order of the other two sides does not matter. The convention is usually
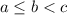though you could easily do
