Answer:
Explanation:
Isolate it by the term of x from one side of the equation.
- Part A. There will be one solution.
- Part B.
4(2x-5)=4
First, divide by 4 from both sides.
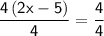
Then, solve.
4/4=1
Rewrite the problem down.
2x-5=1
Add by 5 from both sides.
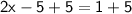
Solve.
1+5=6
2x=6
Divide by 2 from both sides.
2x/2=6/2
Solve.
Divide the numbers from left to right.
6/2=3
x=3
- Therefore, the correct answer is x=3.
I hope this helps you! Let me know if my answer is wrong or not.