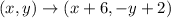Question

Help me out with this

Answer 1

Let's follow the transformations that happen to A, to get to A' and A''.

Point A is at (-5, -2)

It moves to (-5, 2) which is where A' is located. Note the x coordinate stays the same while the y coordinate flips from negative to positive. This must mean we applied a reflection over the x axis.

That rule in general is
`(x, y) \rightarrow (x,-y)`

------------------------------------

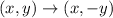
Now compare A'(-5,2) and A''(1,4). We can shift A' 6 units to the right and then 2 units up so we move from A' to A''.

Algebraically this is stated as
`(x,y) \rightarrow (x+6, y+2)`

Whatever the x coordinate is, add 6 to it. For the y coordinate, we add on 2.

Applying that rule to B'(-1,2) gets us to

`(-1,2) \rightarrow (-1\textbf{+6}, 2\textbf{+2}) = (5,4)`

which is the proper location of B''

The same applies to moving C' to C''

`C' = (-5, 0) \rightarrow (-5\textbf{+6}, 0\textbf{+2}) = (1, 2) = C''`

-------------------------------------------

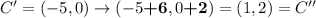
In summary, we started off by reflecting over the x axis. Then we applied the translation rule of "shift to the right 6 units, shift up 2 units".

In terms of algebra, combining the rules
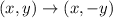`(x,y) \rightarrow (x,-y)` and
`(x,y) \rightarrow (x+6, y+2)` will have us end up with
`(x,y) \rightarrow (x+6, -y+2)`