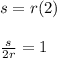Question

Consider the diagram shown. Choose all the true statements.

If Θ = 2 rad, then r > s.

If Θ = 1 rad, then r ≤ s.

If s = 1/2r, then 2Θ = 1.

If s/2r=1, then Θ = 2

Answer 1

If Θ = 1 rad, then r ≤ s

If s = 1/2r, then 2Θ = 1

If s/(2r)=1, then Θ = 2

Explanation:

we know that

The arc length s is equal to

`s=r\theta`

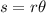
where

r is the radius

`\theta` is the central angle in radians

Verify each statement

case 1) If Θ = 2 rad, then r > s

The statement is false

Because

For Θ = 2 rad

substitute

`s=r(2)\\s=2r`

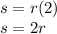
so

`s>r`

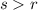
case 2) If Θ = 1 rad, then r ≤ s

The statement is true

Because

For Θ = 1 rad

substitute

`s=r(1)`

`s=r`

so

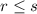`r\leq s` ---> is true

case 3) If s = 1/2r, then 2Θ = 1

The statement is true

Because

For s=1/2r

substitute

`(1)/(2)r=r\theta`

`\theta=(1)/(2)`

`2\theta=1`

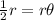
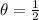
case 4) If s/2r=1, then Θ = 2

The statement is true

Because

For Θ = 2

substitute

`s=r(2)\\\\(s)/(2r)=1`