Question

Use the Parabola tool to graph the quadratic function.

f(x)=3x^2−6x+5

Graph the parabola by first plotting its vertex and then plotting a second point on the parabola.

Answer 1

Given function:
`f(x)=3x^2-6x+5`

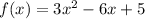
Vertex form:
`y=a(x-h)^2+k`

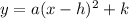
(where
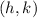`(h, k)` is the vertex)

Expand vertex form:

`y=ax^2-2ahx+ah^2+k`

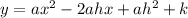
Compare coefficients of given function with expanded vertex form

Comparing coefficient of
`x^2`:

`3=a`

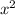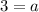
Comparing coefficient of
`x`:

`\ \ \ \ \ -6=-2ah\\\implies-6=-2 \cdot 3h\\\implies -6=-6h\\\implies h=1`

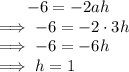
Comparing constant:

`\ \ \ \ \ \ 5=ah^2+k\\\implies5=3(1)^2+k \\\implies 5=3+k\\\implies k=2`

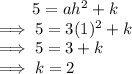
Therefore, the vertex is (1, 2)

As the leading coefficient is positive, the parabola will open upwards.

Additional plot points:

`f(0)=3(0)^2-6(0)+5=5`

`f(2)=3(2)^2-6(2)+5=5`

(0, 5) and (2, 5)

Answer 2

graphed below:

`\sf f(x)=3x^2-6x+5`

• vertex: (1, 2)

• cuts y-axis: (0, 5)