Question

What is the range of f(x) = 3/4x -4

y > –4
{y \ y > 3/4}
y
y < 3/4

Answer 1

The range is the resulting y-values we get after substituting all the possible x-values.

For the given function :
`f(x) = (3)/(4x) -4`

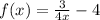
See the attached figure.

The zeros of the denominator at x = 0

The domain is: (-∞,0)∪(0,∞)

The range of the function is the domain of the inverse function of f(x)

y = 3/(4x) - 4

y + 4 = 3/(4x)

4x = 3/(y+4)

`x=(3)/(4(y+4))`

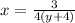
The zeros of the inverse function:

4(y+4) = 0

y + 4 = 0

y = -4

∴ The range is (-∞,-4)∪(-4,∞)

So, the answer is y ∪ y

=========================================

Note: If the given function is :
`f(x) = (3)/(4) x-4`

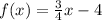
It will be first degree polynomial function.

Both of the domain and the range = all real numbers R