Answer:
Part 1)
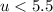
Part 2)
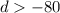
Part 3)

Part 4)
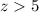
Part 5)
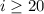
Explanation:
The question is
Solve each inequality for the indicated variable
Part 1) we have
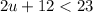
subtract 12 both sides
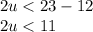
Divide by 2 both sides
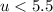
The solution is the interval (-∞,5.5)
In a number line the solution is the shaded area at left of u=5.5 (open circle)
The number 5.5 is not included in the solution
Part 2) we have
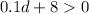
subtract 8 both sides
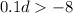
Divide by 0.1 both sides
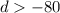
The solution is the interval (-80,∞)
In a number line the solution is the shaded area at right of d=-80 (open circle)
The number -80 is not included in the solution
Part 3) we have
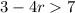
Subtract 3 both sides

Divide by -4 both sides
Remember that, when you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality symbol

The solution is the interval (-∞,-1)
In a number line the solution is the shaded area at left of r=-1.1 (open circle)
The number -1.1 is not included in the solution
Part 4) we have
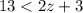
Subtract 3 both sides
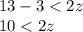
Divide by 2 both sides
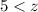
Rewrite
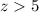
The solution is the interval (5,∞)
In a number line the solution is the shaded area at right of z=5 (open circle)
The number 5 is not included in the solution
Part 5) we have

Subtract 9 both sides
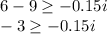
Divide by -0.15 both sides
Remember that, when you multiply or divide both sides of an inequality by a negative number, you must reverse the inequality symbol
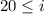
Rewrite
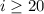
The solution is the interval [20,∞)
In a number line the solution is the shaded area at right of i=20 (closed circle)
The number 20 is included in the solution