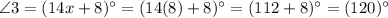Question

Two parallel lines are cut by a transversal. Angle 1 measures (4x + 28)°, and the angle adjacent to the alternate exterior angle with angle 1 measures (14x + 8)°. What is the value of x?

Answer 1

The value of x is 8

Explanation:

Answer 2

The value of x is 8

Explanation:

In the figure below,

The alternate exterior angles are 1 and 2

Alternate Exterior Angles are a pair of angles that lie on the outer side of each of those two lines but on opposite sides of the transversal and they are equal

Also angle 2 and 3 are adjacent and supplementary angle and their sum is equal to 180 degrees

Given that

`\angle 1 = (4x + 28)^(\circ)`

`\angle 3 = (14x + 8)^(\circ)`

Now we know that

`\angle 2 + \angle 3 = 180 ^(\circ)`

`\angle 2 +(14x+8) = 180`

`\angle 2 = 180 - 14x -8`

`\angle 2 = 172 - 14x`

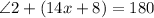
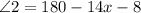
We also know that

`\angle 1 = \angle 2`

`4x + 28 = 172 -14x`

`4x + 14x = 172 - 28`

`18x = 144`

`x =(144)/(18)`

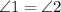
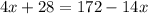
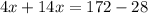
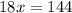
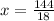
x = 8

Now

`\angle 1 = (4x+28)^(\circ) = (4(8) +28)^(\circ) = (32 +28)^(\circ) =(60)^(\circ)`

`\angle 3= (14x+8)^(\circ) = (14(8) +8)^(\circ) = (112 +8)^(\circ) =(120)^(\circ)`