Question

ASAP PLEASE !!!!!

Two trains leave a station on different tracks. The tracks make an angle of 130°, with the station as a vertex. The first train
travels 100 km and makes its first stop at point A, while the second train travels 200 km and makes it first stop at point B.
How far apart are the trains when both are at their first stop? Round the answer to the nearest integer.

Answer 1

D. 275 km

Explanation:

Answer 2

The trains are 275 km apart when both are at their first stop

Solution:

The tracks make an angle of 130°, with the station as a vertex

Therefore, from given figure in question,

Angle at station = 130 degree

Let "c" be the point at station

The first train travels 100 km and makes its first stop at point A

Distance between A and station c = 100 km

Let a = 100 km

The second train travels 200 km and makes it first stop at point B

Distance between B and station c = 200 km

Let b = 200 km

We have to find the value of "d"

We can use the law of cosine

The square of a side of a plane triangle equals the sum of the squares of the remaining sides minus twice the product of those sides and the cosine of the angle between them.

From given figure in question,

Side opposite "d" to 130 degree is equal to sum of square of other sides a and b minus twice the product of those sides and the cosine of the angle between them which is 130 degrees

Therefore,

`d^2 = a^2 + b^2 - 2ab\ cos\ d`

`d^2 = 100^2 + 200^2 - 2(100)(200)cos 130\\\\d^2 = 10000 + 40000 - 40000cos 130\\\\d^2 = 50000 - 40000 * -0.6427\\\\d^2 = 50000 + 25711.5\\\\d^2 = 75711.5\\\\\text{Take square root on both sides }\\\\d = 275.15 \approx 275`

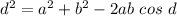
Thus trains are 275 km apart when both are at their first stop