Answer:
F = 1076 N
Step-by-step explanation:
given,
small piston area, a = 0.075 m²
large piston area, A = 0.237 m²
weight on the large piston, W = 3400 N
force applied on the second piston, F = ?
using pascal law for the force calculation
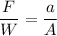
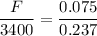
F = 0.3165 x 3400
F = 1076 N
The force applied to the small piston in order to lift the engine is equal to 1076 N.