The LCM of
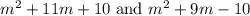 is
is

Solution:
On factorising
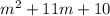 we get,
we get,
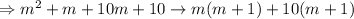
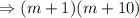
Therefore, the factors of m^2+11m+10 are (m+1)(m+10)
On factorising
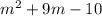 we get,
we get,
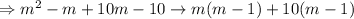
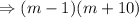
Therefore, the factors of
 are
are

So, the LCM of both the given expressions will be

Steps to find the LCM (Least Common Multiple) of two given monomials or polynomials:
Step 1: Find all the factors of all the expressions being multiplied.
Step 2: Multiply together one of each unique factor, and the repeat factors with the highest exponents.