Question

A moose population is growing exponentially following the pattern in the table shown below. Assuming that the pattern continues, what will be the population of moose after 12 years? Round your answer to the nearest whole number.

Answer 1

The population of moose after 12 years will be 7,692

Explanation:

Exponential Growth

Some functions are adequate for modeling real-life events such as population growth, where the exponential function comes handy. The general form of an exponential function is

`f(x)=a.b^x`

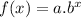
Where a and b are constants to be determined according to the available field data. We are provided a table of values relating the time in years and the moose population.

We'll pick the first two points (0,40) and (1,62). Replacing them into the general function, we'll get the values of a and b

`f(0)=a.b^0=40`

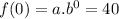
which gives:

`a=40`

`f(1)=40.b^1=62`

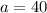
Solving for b

`b=62/40`

`b=1.55`

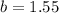
The model function is

`f(x)=40.(1.55)^x`

Testing for other values of the table:

`f(2)=40.(1.55)^2=96`

`f(3)=40.(1.55)^3=149`

`f(4)=40.(1.55)^4=231`

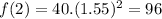
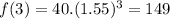
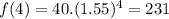
As seen, the function is adequate to model the moose population. We are now required to find

`f(12)=40.(1.55)^(12)=7,692`

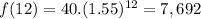
The population of moose after 12 years will be 7,692