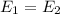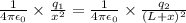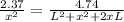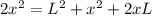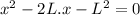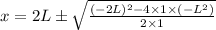Answer:
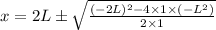
Step-by-step explanation:
Given:
- charge on first particle,
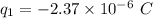
- charge on the second particle,
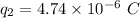
- distance between the two charges = L
Now the third charge must be placed on the line joining the two charges at a distance where the intensity of electric field is same for both the charges that point will not lie between the two charges because they are opposite in nature.