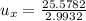Question

Henrietta is going off to her physics class, jogging down the sidewalk at a speed of 3.20 m/s. Her husband Bruce suddenly realizes that she left in such a hurry that she forgot her lunch of bagels, so he runs to the window of their apartment, which is a height 43.9 m above the street level and directly above the sidewalk, to throw them to her. Bruce throws them horizontally at a time 5.00 s after Henrietta has passed below the window, and she catches them on the run. You can ignore air resistance.With what initial speed must Bruce throw the bagels so Henrietta can catch them just before they hit the ground? Where is Henrietta when she catches the bagels?

Answer 1

`u_x=8.5454\ m.s^(-1)`

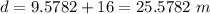`d=9.5782+16=25.5782\ m` was the her position ahead from her window when she caught the object.

Step-by-step explanation:

Given:

• speed of walking of Henrietta,
  `v_w=3.2\ m.s^(-1)`

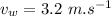
• height of projection of projectile,
  `h=43.9\ m`

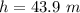
• Horizontal distance between the window and Henrietta when the projectile was launched:

`r=3.2* 5`

`r=16\ m`

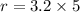
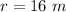
• Since the projectile was thrown at the time when she had passed below the window 5 seconds ago.

Since the projectile was thrown horizontally therefore the vertical component of velocity is zero.

Now the time taken for the object to reach to Henrietta ignoring the height where she catches:

`h=u_x.t+(1)/(2) * g.t^2`

`43.9=0+(1)/(2) * 9.8* t^2`

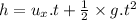
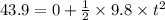
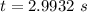`t=2.9932\ s` is the time taken by the projectile to reach Henrietta.

Now the distance further walked by Henrietta in the above time from the point where she was when the projectile was launched:

`\Delta d=v_w* t`

`\Delta d=9.5782\ m`

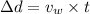
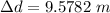
Now the total horizontal distance from the window to Henrietta when the projectile reached her:

`d=\Delta d+r`

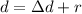
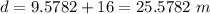`d=9.5782+16=25.5782\ m` was the her position ahead from her window when she caught the object.

Now the initial horizontal velocity of launch of the projectile:

`u_x=(d)/(t)`

`u_x=(25.5782)/(2.9932)`

`u_x=8.5454\ m.s^(-1)`