Question

A Carnot heat engine receives 3,200 kJ/s of heat from a high temperature source at 825 ℃ and rejects heat to a cold temperature sink at 15 ℃. Please solve following questions:

a. What is the thermal efficiency of this engine?
b. What is the power delivered by the engine in watts?
c. At what rate is heat rejected to the cold temperature sink?
d. What is the entropy change of the sink?

Answer 1

a.
`\eta_(th)=0.7377=73.77\%`

b.
`P=2360655.7377\ W`

c.
`Q_o=839344.2622\ W`

d.
`\Delta s=2914.3897\ J.K^(-1)`

Step-by-step explanation:

Given:

• temperature of the source,
  `T_H=825+273=1098\ K`

• heat received from the source,
  `Q_i=3200000\ J.s^(-1)`

• temperature of the sink,
  `T_L=15+273=288\ K`

a.

Since the engine is a Carnot engine:

`\eta_(th)=1-(T_L)/(T_H)`

`\eta_(th)=1-(288)/(1098)`

`\eta_(th)=0.7377=73.77\%`

b.

Now the power delivered:

since here we are given with the rate of heat transfer

`P=\eta_(th)* Q_i`

`P=0.7377* 3200000`

`P=2360655.7377\ W`

c.

rate of heat rejection to the sink:

`Q_o=Q_i-P`

`Q_o=3200000-2360655.73770491808`

`Q_o=839344.2622\ W`

d.

`\Delta s=(Q_o)/(T_L)`

`\Delta s=(839344.2622)/(288)`

`\Delta s=2914.3897\ J.K^(-1)`

Answer 2

Step-by-step explanation:

Given:

source temperature T1= 825° C = 1099 K

Sink temperature T2= 15°C = 288 K

Heat Supplied to the engine Qs= 3200 KW

a) Efficiency of a Carnot engine is

`\eta =1-(T_1)/(T_2)`

`=1-(1099)/(288)`

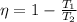
=0.7379

=73.79%

b)

`\eta= (Power delivered)/(power recieved)`

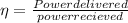
let W be the powe delivered

`0.7379= (W)/(3200)`

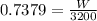
W= 2361.408 KW

c) Heat rejected to the cold temperature Qr= Qs-W

= 3200-2361.408=838.60 KW

d) Entropy change in the sink

`\Delta S= (Qr)/(T_(sink))`

=838.60/288= 2.911 W/K