Question

Find parametric equations for the following curve. Include an interval for the parameter values. The line that passes through the points (- 4, 3) and (2, - 5). oriented in the direction of increasing x.

Choose the correct set of parametric equations and interval below.

A. x = -4 + 3t, y = 3 - 4t: - 2 lessthanorequalto t lessthanorequalto 3

B. x = - 4 + 3t, y = 3 - 4t: - infinity < t < infinity

C. x = 3 - 4t, y = - 4 + 3t: - infinity < t < infinity

D. x = 3 - 4t, y = - 4+ 3t: -2 lessthanorequalto t lessthanorequalto 3

Answer 1

A. x = -4 + 3t, y = 3 - 4t: - 2 lessthanorequalto t lessthanorequalto 3

Explanation:

Given that a line in two dimension passes through (-4,3) and (2,-5) oriented in the direction of increasing x

We can write the line equation in parametric form as

`(x-x_1)/(x_2-x_1) =(y-y_1)/(y_2-y_1) \\(x+4)/(6) =(y-3)/(-8) =t\\x=-4+6t\\y = 3-8t`

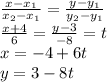
The values of t when x=-4 is 0 and when x =2 is 1

So t varies from 0 to 1

If instead of t we give t' say which is t +2

then we have

t he parametric equations as

x =-4+3t and y = 3-4t

For x=-4, t =2 and for x = 2 , t =3

So option A is right.