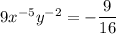Question

Evaluate the expression when x = -1 and y = 4. 9x^-5y^-2y

A) 9/64
B) 9/16
C) -9/64
D) -9/16

Answer 1

The correct option is D) -9/16

Therefore the final expression when X is equal to -1 and Y is equal to 4 is

`9x^(-5)y^(-2)=-(9)/(16)`

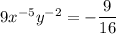
Explanation:

Given:

`9x^(-5)y^(-2)`

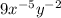
Evaluate when x = -1 and y = 4

Solution:

When x = -1 and y = 4 we hane

`9x^(-5)y^(-2)=9(-1)^(-5)(4)^(-2)`

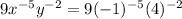
Identity we have

`x^(-a)=(1)/(x^(a))`

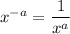
As we know minus sign multiplied by odd number of times the number is multiplied and the assign remain same that is minus. Therefore,

`(-1)^(5)=-1* -1* -1* -1* -1\\(-1)^(5)=-1`

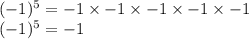
Now using the above identity we get

`9x^(-5)y^(-2)=(9)/((-1)^(5))* (1)/((4)^(2))`

`9x^(-5)y^(-2)=(9)/(-1)*(1)/(16)`

`9x^(-5)y^(-2)=-(9)/(16)`

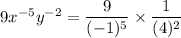
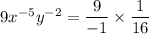
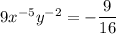
Therefore the final expression when X is equal to -1 and Y is equal to 4 is

`9x^(-5)y^(-2)=-(9)/(16)`