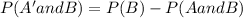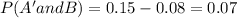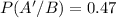Question

Suppose that 20% of adults practices a gluten-free diet, 15% of adults practice a dairy-free diet, and 8% of adults practice both of these diets. One adult is selected at random.

a. Given a random individual practices a glute-free diet, what is the probability they practice a dairy-free diet?

b. Are events "practices a gluten-free diet" and "practices a dairy-free diet" independent?

c. Given a random individual practices a dairy-free diet, what is the probability they do not practice a gluten free diet?

Answer 1

a. 0.4

b. Not independent

c. 0.47

Explanation:

Answer 2

a. 0.4

b. Not independent events

c. 0.47

Explanation:

Let A= Practices Gluten free diet

B= Practices Dairy free diet

A and B= Practices Both diets

P(A)=0.20

P(B)=0.15

P(A and B)=0.08

a.

`P(B/A)=(P(A and B))/(P(A))`

`P(B/A)=(0.08)/(2)`

`P(B/A)=0.40`

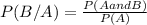
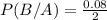
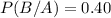
b.

The two events are independent if P(B/A) =P(B) or P(A/B)=P(A)

As, P(B/A) ≠P(B)

0.4≠0.15

So, the event gluten free diet and dairy free diet are dependent events.

c.

`P(A'/B)=(P(A' and B))/(P(B))`

`P(A'and B)= P(B)-P(A and B)`

`P(A' and B)=0.15-0.08=0.07`

`P(A'/B)=(P(A' and B))/(P(B))`

`P(A'/B)=(0.07)/(0.15)`

`P(A'/B)=0.47`