Question

Working as an insurance salesperson, Ilya earns a base salary and a commission on each new policy, so Ilya’s weekly income, II, depends on the number of new policies, n, he sells during the week. Last week he sold 3 new policies, and earned $760 for the week. The week before, he sold 5 new policies, and earned $920. Find an equation for I(n), and interpret the meaning of the components of the equation.

Answer 1

l(n) = 80n + 520

Explanation:

From the information given in the question, there is a relationship between the number of new policy sold, n, and earning, I

For 3 new policies, he earned $760

For 5 new policies, he earned $920.

The rate of change of IIya's earning with respect to number of new policy sales is

`m = (dI)/(dn)`

`m = (920 - 760)/(5 - 3)`

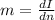
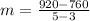
m = $160 / 2 policies

m = $80 / policy

The linear equation for the relationship is;

l(n) = mn + b

I(n) is Ilya’s weekly income which is a function of the number of new policies, n

m is the rate of change of I with respect to n

n is the number of new policies,

b is the intial function which is IIya's income when n equals zero

Recall, Ilya earns a commission of $80 for each policy sold during the week. (m = $80 per policy)

l(n) = 80n + b

To complete the relationship l, we need to calculate the initial value b.

For 3 new policies, he earned $760,

760 = 80(3) + b

760 = 240 + b

b = 760 - 520

b = 520

The final equation is l(n) = 80n + 520

From the final equation, we can deduce that Ilya’s weekly salary is $520 and he earns an additional $80 commission for each new policy sold.