Question

A positron is an elementary particle identical to an electron except that its charge is . An electron and a positron can rotate about their center of mass as if they were a dumbbell connected by a massless rod.What is the orbital frequency for an electron and a positron 1.50 apart?

Answer 1

Step-by-step explanation:

According to the energy conservation,

`F_(centripetal) = F_(electric)`

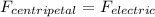
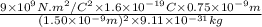
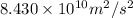
`(mv^(2))/(r) = (kq^(2))/(d^(2))`

`v^(2) = (kq^(2)r)/(d^(2)m)`

=
`(9 * 10^(9) N.m^(2)/C^(2) * 1.6 * 10^(-19) C * 0.75 * 10^(-9) m)/((1.50 * 10^(-9)m)^(2) * 9.11 * 10^(-31) kg)`

=
`8.430 * 10^(10) m^(2)/s^(2)`

v =
`\sqrt{8.430 * 10^(10) m^(2)/s^(2)}`

=
`2.903 * 10^(5) m/s`

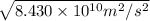
Formula for distance from the orbit is as follows.

S =
`2 \pi r`

=
`2 * 3.14 * 0.75 * 10^(-9) m`

=
`4.71 * 10^(-9) m`

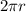
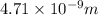
Now, relation between time and distance is as follows.

T =
`(S)/(v)`

`(1)/(f) = (S)/(v)`

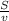
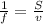
or, f =
`(v)/(S)`

=
`(2.903 * 10^(5) m/s)/(4.71 * 10^(-9) m)`

=
`6.164 * 10^(13) Hz`

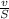
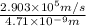
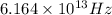
Thus, we can conclude that the orbital frequency for an electron and a positron that is 1.50 apart is
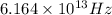`6.164 * 10^(13) Hz`.