Question

A positively charged particle initially at rest on the ground accelerates upward to 160 m/s in 2.10 s. The particle has a charge-to-mass ratio of 0.100 C/kg and the electric field in this region is constant and uniform.What are the magnitude and direction of the electric field? Express your answer to two significant digits and include the appropriate units.

Answer 1

E = 8.6 x 10² N/C

Step-by-step explanation:

given,

initial speed of charge,u = 0 m/s

final speed of charge,v = 160 m/s

time,t = 2.1 s

charge-to-mass ratio = 0.100 C/kg

Electric field of the region = ?

Acceleration of the charge

`a = (v-u)/(t)`

`a = (160 - 0)/(2.1)`

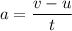
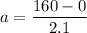
a = 76.19 m/s²

specific charge =
`(q)/(m) = 0.1`

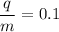
now,

Electric field,

`E = (F)/(q)`

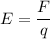
charge is moving upwards so,

`E = ((a + g))/((q)/(m))`

`E = ((76.19+9.8))/(0.1)`

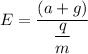
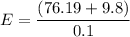
E = 860 N/C

electric field , E = 8.6 x 10² N/C

hence, the magnitude of electric field is equal to E = 8.6 x 10² N/C

Answer 2

The magnitude of the electric field is
`8.6*10^(2)\ N/C`

Step-by-step explanation:

Given that,

Time t = 2.10 s

Speed = 160 m/s

Specific charge =Ratio of charge to mass = 0.100 C/kg

We need to calculate the acceleration

Using equation of motion

`a=(v-u)/(t)`

Put the value into the formula

`a=(160-0)/(2.10)`

`a=76.19\ m/s^2`

We need to calculate the magnitude of the electric field

Using formula of electric field

`E=(F)/(q)`

`E=(ma)/(q)`

`E=(a+g)/((q)/(m))`

Put the value into the formula

`E=(76.19+9.8)/(0.100)`

`E=8.6*10^(2)\ N/C`

The direction is upward.

Hence, The magnitude of the electric field is
`8.6*10^(2)\ N/C`