Answer:
a. The sampling distribution for the sample mean will be skewed to the left centered at the average u, and standard deviation will be ∅
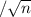
b. The sample distribution will be normal in shape and will be centered at the average u, . standard deviation will be ∅
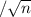 1
1
c. As the size of the sample increases, the sample distribution should draw near and resemble the distribution of the population
Step-by-step explanation:
A sample is chosen randomly from a population that was strongly skewed to the left. a) Describe the sampling distribution model for the sample mean if the sample size is small. b) If we make the sample larger, what happens to the sampling distribution model’s shape, center, and spread? c) As we make the sample larger, what happens to the expected distribution of the data in the sample?
The following answers will march the questions above:
a. The sampling distribution for the sample mean will be skewed to the left centered at the average u, and standard deviation will be ∅
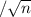
b. The sample distribution will be normal in shape and will be centered at the average u, . standard deviation will be ∅
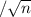 1
1
c. As the size of the sample increases, the sample distribution should draw near and resemble the distribution of the population