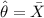Answer:
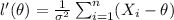
And then the maximum occurs when
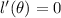 , and that is only satisfied if and only if:
, and that is only satisfied if and only if:
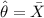
Explanation:
For this case we have a random sample
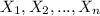 where
where
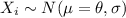 where
where
 is fixed. And we want to show that the maximum likehood estimator for
is fixed. And we want to show that the maximum likehood estimator for
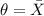 .
.
The first step is obtain the probability distribution function for the random variable X. For this case each
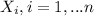 have the following density function:
have the following density function:
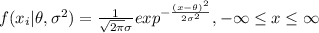
The likehood function is given by:
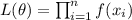
Assuming independence between the random sample, and replacing the density function we have this:
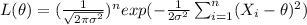
Taking the natural log on btoh sides we got:
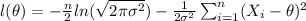
Now if we take the derivate respect
 we will see this:
we will see this:
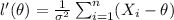
And then the maximum occurs when
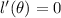 , and that is only satisfied if and only if:
, and that is only satisfied if and only if: