Question

Water is withdrawn from a conical reservoir, 8 feet in diameter and 10 feet deep (vertex down) at the constant rate of 5 ft³/min. How fast is the water level falling when the depth of the water in the reservoir is 5 ft? (
`V = (1)/(3) \pi r^2h`).

Answer 1

Water level in the reservoir is falling at the rate of 0.398 ft per minute.

Explanation:

From the figure attached,

Water level in the reservoir has been given as 10 feet and radius of the reservoir is 4 feet.

Let the level of water in the reservoir after time t is h where radius of the water level becomes r.

ΔABE and ΔCDE are similar.

Therefore, their corresponding sides will be in the same ratio.

`(r)/(h)=(4)/(10)`

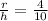
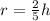`r=(2)/(5)h` --------(1)

Now volume of the water V =
`(1)/(3)\pi r^(2)h`

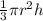
From equation (1),

V =
`(1)/(3)\pi ((2)/(5)h)^(2) h`

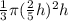
V =
`(4\pi h^(2)* h)/(75)`

`(dV)/(dt)=(4\pi )/(75)* (d)/(dt)(h^(3))`

`(dV)/(dt)=(4\pi )/(75)* (3h^(2))(dh)/(dt)`

`(dV)/(dt)=(12\pi h^(2))/(75)* (dh)/(dt)`

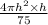
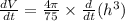
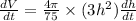
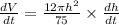
Since
`(dV)/(dt)=5` feet³ per minute and h = 5 feet

`5=(12\pi (5)^(2))/(75)* (dh)/(dt)`

`5=4\pi (dh)/(dt)`

`(dh)/(dt)=(5)/(4\pi)`

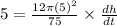
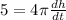
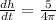
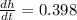`(dh)/(dt)=0.398` feet per minute

Therefore, water level in the reservoir is falling at the rate of 0.398 feet per minute.