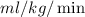Question

An article reported the following data on oxygen consumption (mL/kg/min) for a sample of ten firefighters performing a fire-suppression simulation: 28.6 49.4 30.3 28.2 28.9 26.4 33.8 29.9 23.5 30.2Compute the following. (Round your answers to four decimal places.) a. The sample range mL/kg/minb. The sample variance s2 from the definition (i.e., by first computing deviations, then squaring them, etc.) mL2/kg2/min2c. The sample standard deviation mL/kg/mind. s2 using the shortcut method mL2/kg2/min

Answer 1

a) The sample range 25.9
`ml\slash kg\slash \min`

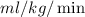
b) The sample variance is 49.344
`ml^2 \slash kg^2 \slash min^2`

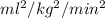
c) The sample standard deviation 7.0245
`ml\slash kg\slash \min`

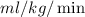
Explanation:

We are given the following data on oxygen consumption (mL/kg/min):

28.6, 49.4, 30.3, 28.2, 28.9, 26.4, 33.8, 29.9, 23.5, 30.2

a) The sample range

Range = Maximum - Minimum

`\text{Range} = 49.4 - 23.5 = 25.9`

The sample range 25.9
`ml\slash kg\slash \min`

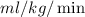
b) The sample variance

`\text{Variance} = \displaystyle\frac{\sum (x_i -\bar{x})^2}{n-1}`

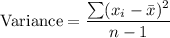
where
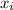`x_i` are data points,
`\bar{x}` is the mean and n is the number of observations.

`Mean = \displaystyle\frac{\text{Sum of all observations}}{\text{Total number of observation}}`

`Mean =\displaystyle(309.2)/(10) = 30.92`

Sum of squares of differences =

5.3824 + 341.5104 + 0.3844 + 7.3984 + 4.0804 + 20.4304 + 8.2944 + 1.0404 + 55.0564 + 0.5184 = 444.096

`s^2 = (444.096)/(9) = 49.344`

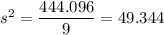
The sample variance is 49.344
`ml^2 \slash kg^2 \slash min^2`

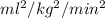
c) The sample standard deviation

It is the square root of sample variance.

`s = √(s^2) = √(49.344) = 7.0245`

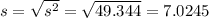
The sample standard deviation 7.0245
`ml\slash kg\slash \min`