Answer:
Part A:
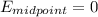
Part B:

Step-by-step explanation:
Part A:
Formula of Electric Field Strength:
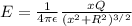
Where:
x is the distance from the ring
R is the radius of the ring
 is constant permittivity of free space=8.854*10^-12 farads/meter
is constant permittivity of free space=8.854*10^-12 farads/meter
Q is the charge
For right Ring E at the midpoint can be calculated as:
x for right plate=25/2=12.5 cm=0.125 m
Radius=R=10/2=5 cm=0.05 m
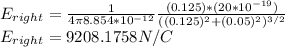
For Left Ring E at the midpoint can be calculated as:
Since charge on both plates is +ve and same in magnitude, the electric field will be same for both plates.

Electric Field at midpoint:
Both rings have same magnitude but the direction of fields will be opposite as they have same charge on them.

Part B:
At center of left ring:
Due to left ring Electric field at center is zero because x=0.
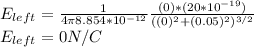
Due to right ring Electric field at center of left ring:
Now: x=25 cm= o.25 m (To the center of left ring)
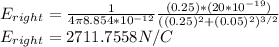
Electric Field Strength at center of left ring is same as that of right ring.
