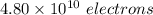Question

Two parallel square metal plates that are 1.5 cm and 22 cm on each side carry equal but opposite charges uniformly spread out over their facing surfaces. How many excess electrons are on the negative surface if the electric field between the plates has a magnitude of 18,000 N/C? (k = 1/4 pi epsilon_0 = 9.0 times 10^9 N m^2/C^2, e = 1.6 times 10^-19 C)

Answer 1

The number of excess electrons are on the negative surface is
`4.80*10^(10)\ electrons`

Step-by-step explanation:

Given that,

Distance =1.5 cm

Side = 22 cm

Electric field = 18000 N/C

We need to calculate the capacitance in the metal plates

Using formula of capacitance

`C=(\epsilon_(0)A)/(d)`

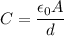
Put the value into the formula

`C=(8.85*10^(-12)*(22*10^(-2))^2)/(1.5*10^(-2))`

`C=0.285*10^(-10)\ F`

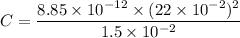
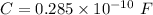
We need to calculate the potential

Using formula of potential

`V=Ed`

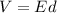
Put the value into the formula

`V=18000*1.5*10^(-2)\ V`

`V=270\ V`

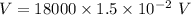
We need to calculate the charge

Using formula of charge

`Q=CV`

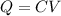
Put the value into the formula

`Q=0.285*10^(-10)*270`

`Q=76.95*10^(-10)\ C`

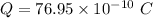
Here, the charge on both the positive and negative plates

`Q=+76.95*10^(-10)\ C`

`Q=-76.95*10^(-10)\ C`

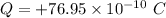
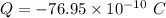
We need to calculate the number of excess electrons are on the negative surface

Using formula of number of electrons

`n=(q)/(e)`

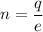
Put the value into the formula

`n=(76.95*10^(-10))/(1.6*10^(-19))`

`n=4.80*10^(10)\ electrons`

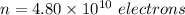
Hence, The number of excess electrons are on the negative surface is
`4.80*10^(10)\ electrons`