Question

A vertical spring with spring stiffness constant 305 N/m oscillates with an amplitude of 28.0 cm when 0.235 kg hangs from it. The mass passes through the equilibrium point (y=0) with positive velocity at t=0. Positive direction of y-axis is downward.

Part A

What equation describes this motion as a function of time?

Part B

At what time will the spring stretch to its maximum length at first time?

Part C

At what time will the spring shrink to its minimum length at first time?

Answer 1

`y(t)=0.28sin(36.02599t)`

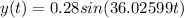
0.0436 s

0.1308 s

Step-by-step explanation:

A = Amplitude = 28 cm

m = Mass = 0.235 kg

k = Spring constant = 305 N/m

The equation which describes motion as a function of time is given by

`y(t)=Asin(\omega t)`

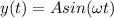
Angular speed is given by

`\omega=\sqrt{(k)/(m)}\\\Rightarrow \omega=\sqrt{(305)/(0.235)}\\\Rightarrow \omega=36.02599\ rad/s`

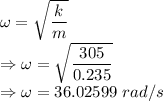
The equation is

`\mathbf{y(t)=0.28sin(36.02599t)}`

Maximum length will be at amplitude

Amplitude is given by

`A=Asin(\omega t)`

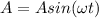
here

`\omega t=(\pi)/(2)\\\Rightarrow t=(\pi)/(2* 36.02599)\\\Rightarrow t=0.0436\ s`

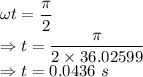
The time to stretch to maximum length is 0.0436 s

At minimum length

`y(t)=-A\\\Rightarrow -A=Asin\omega t`

`\omega t=(3\pi)/(2)\\\Rightarrow t=(3\pi)/(2\omega)\\\Rightarrow t=(3\pi)/(2* 36.02599)\\\Rightarrow t=0.1308\ s`

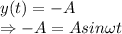
The time will the spring shrink to its minimum length at first time is 0.1308 s