Question

An electron and a proton are each placed at rest in a uniform electric field of magnitude 560 N/C. Calculate the speed of each particle 46.0 ns after being released. electron 4.5e^-6 Incorrect.

Answer 1

The speed of electron is
`v=4.52* 10^6\ m/s` and the speed of proton is 2468.02 m/s.

Step-by-step explanation:

Given that,

Electric field, E = 560 N/C

To find,

The speed of each particle (electrons and proton) 46.0 ns after being released.

Solution,

For electron,

The electric force is given by :

`F=qE`

`F=1.6* 10^(-19)* 560=8.96* 10^(-17)\ N`

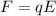
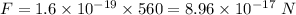
Let v is the speed of electron. It can be calculated using first equation of motion as :

`v=u+at`

u = 0 (at rest)

`v=(F)/(m)t`

`v=(8.96* 10^(-17))/(9.1* 10^(-31))* 46* 10^(-9)`

`v=4.52* 10^6\ m/s`

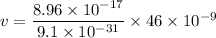
For proton,

The electric force is given by :

`F=qE`

`F=1.6* 10^(-19)* 560=8.96* 10^(-17)\ N`

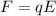
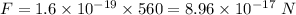
Let v is the speed of electron. It can be calculated using first equation of motion as :

`v=u+at`

u = 0 (at rest)

`v=(F)/(m)t`

`v=(8.96* 10^(-17))/(1.67* 10^(-27))* 46* 10^(-9)`

`v=2468.02\ m/s`

So, the speed of electron is
`v=4.52* 10^6\ m/s` and the speed of proton is 2468.02 m/s. Therefore, this is the required solution.