Answer:
The score for both exams 88 is above the 90 percentile, so then Brynne qualified for honors. See the explanation below.
Step-by-step explanation:
Assuming the following question:"At Westtown High School, the mean score on the French final examination was 81 with a standard deviation of 5, while the mean score on the Spanish final examination was 72 with a standard deviation of 12.
To earn a language honor at graduation, students must score in the 90th percentile on all their language final exams. Brynne scored 88 on both the French exam and the Spanish exam. Is Brynne qualified for honors?"
Previous concepts
Normal distribution, is a "probability distribution that is symmetric about the mean, showing that data near the mean are more frequent in occurrence than data far from the mean".
The Z-score is "a numerical measurement used in statistics of a value's relationship to the mean (average) of a group of values, measured in terms of standard deviations from the mean".
French case
Let X the random variable that represent the scores for the French exam of a population, and for this case we know the distribution for X is given by:
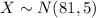
Where
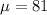 and
and
![\sigma=5[/tex<strong>] </strong></p><p>For this part we want to find a value a, such that we satisfy this condition: </p><p>[tex]P(X>a)=0.1]() (a)
(a)
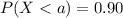 (b)
(b)
Both conditions are equivalent on this case. We can use the z score again in order to find the value a.
As we can see on the figure attached the z value that satisfy the condition with 0.90 of the area on the left and 0.1 of the area on the right it's z=1.28. On this case P(Z<1.28)=0.90 and P(z>1.28)=0.1
If we use condition (b) from previous we have this:
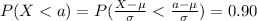
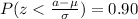
But we know which value of z satisfy the previous equation so then we can do this:
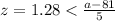
And if we solve for a we got
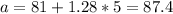
So the value for the scores that separates the bottom 90% of data from the top 10% is 87.4 (90th percentile).
And since the score of Brynne is 88 is above the 90 percentile
Spanish case
Let X the random variable that represent the scores for the Spanish exam of a population, and for this case we know the distribution for X is given by:

Where
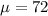 and
and
![\sigma=12[/tex<strong>] </strong></p><p>For this part we want to find a value a, such that we satisfy this condition: </p><p>[tex]P(X>a)=0.1]() (a)
(a)
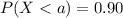 (b)
(b)
Both conditions are equivalent on this case. We can use the z score again in order to find the value a.
As we can see on the figure attached the z value that satisfy the condition with 0.90 of the area on the left and 0.1 of the area on the right it's z=1.28. On this case P(Z<1.28)=0.90 and P(z>1.28)=0.1
If we use condition (b) from previous we have this:
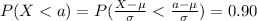
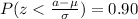
But we know which value of z satisfy the previous equation so then we can do this:
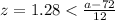
And if we solve for a we got
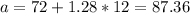
So the value for the scores that separates the bottom 90% of data from the top 10% is 87.36 (90th percentile).
And since the score of Brynne is 88 is above the 90 percentile