Answer:
There are 165 ways to distribute the blackboards between the schools. If at least 1 blackboard goes to each school, then we only have 35 ways.
Explanation:
Essentially, this is a problem of balls and sticks. The 8 identical blackboards can be represented as 8 balls, and you assign them to each school by using 3 sticks. Basically each school receives an amount of blackboards equivalent to the amount of balls between 2 sticks: The first school gets all the balls before the first stick, the second school gets all the balls between stick 1 and stick 2, the third school gets the balls between sticks 2 and 3 and the last school gets all remaining balls.
The problem reduces to take 11 consecutive spots which we will use to localize the balls and the sticks and select 3 places to put the sticks. The amount of ways to do this is
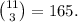 As a result, we have 165 ways to distribute the blackboards.
As a result, we have 165 ways to distribute the blackboards.
If each school needs at least 1 blackboard you can give 1 blackbooard to each of them first and distribute the remaining 4 the same way we did before. This time there will be 4 balls and 3 sticks, so we have to put 3 sticks in 7 spaces (if a school takes what it is between 2 sticks that doesnt have balls between, then that school only gets the first blackboard we assigned to it previously). The amount of ways to localize the sticks is
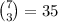 . Thus, there are only 35 ways to distribute the blackboards in this case.
. Thus, there are only 35 ways to distribute the blackboards in this case.