Question

Which of the graphs below correctly solves for x in the equation −x2 − 3x − 1 = −x − 4?

Graph of quadratic opening downward and linear sloping up to the right. They intersect at point negative 4, negative 2 and point 0, 2.
Graph of quadratic opening upward and linear sloping up to the right. They intersect at point 0, 2 and point 4, 6.
Graph of quadratic opening downward and linear sloping up to the left. They intersect at point negative 3, negative 1 and point 1, negative 5.
Graph of quadratic opening upward and linear sloping up to the right. They intersect at point 2, 0.

Answer 1

Answer: C is the correct choice

Explanation:

Answer 2

Graph of quadratic opening downward and linear sloping up to the left. They intersect at point negative 3, negative 1 and point 1, negative 5

Explanation:

we have

`-x^(2) -3x-1=-x-4`

we can separate the expression above into two equations

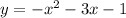`y=-x^(2) -3x-1` ----> equation A

This is a quadratic equation ( vertical parabola) open downward (the leading coefficient is negative)

`y=-x-4` ----> equation B

This is a linear equation with negative slope (decreasing function).so linear sloping up to the left

The solution of the original expression are the x-coordinates of the intersection point both graphs

using a graphing tool

The intersection points are (-3,-1) and (1,-5)

see the attached figure