Question

The radioactive substance uranium-240 has a half-life of 14 hours. The amount At of a sample of uranium-240 remaining (in grams) after t hours is given by the following exponential function.


`A(t) = 2800.((1)/(2))^{(t)/(14)}`
Find the amount of the sample remaining after 9 hours and after 40 hours.
Round your answers to the nearest gram as necessary.
Amount after 9hours: ______ grams
Amount after 40 hours: ______ grams

Answer 1

Amount after 9 hours: 1793 grams

Amount after 40 hours: 386 grams

Explanation:

Given exponential function, that shows the amount of radioactive substance uranium-240 after t hours,

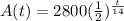`A(t)=2800((1)/(2))^(t)/(14)` ......(1)

Substitute t=9 in equation (1),

The amount of substance after 9 hours is,

`A(9)=2800((1)/(2) )^(9)/(14)`

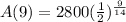
≈ 1793 grams ( Using calculator )

Again, substitute t=40 in equation (1),

The amount of substance after 40 hours is,

`A(40)= 2800((1)/(2))^{(40)/(14) }`

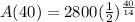
≈ 386 grams.