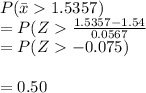Answer:
0.50
Explanation:
Given that a study of rush-hour traffic in San Francisco counts the number of people in each car entering a freeway at a suburban interchange. Suppose that this count has mean 1.5 and standard deviation 0.75 in the population of all cars that enter at this interchange during rush hours.
No of cars per hour = 700
700 randomly selected cars at this freeway entrance will carry more than 1075 people is equivalent to
mean of persons in 700 cars >
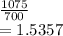
As per central limit theorem sample mean follows normal for large samples randomly drawn.
So here mean follows a normal distribution with mean = 1.5 and std error =
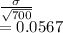
Required probability =