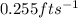Question

The position of a particle on the x-axis at time t, t > 0, is s(t) = ln(t) with t measured in seconds and s(t) measured in feet. What is the average velocity of the particle for e ≤ t ≤ 2e?

Answer 1

`V_(avg) = (ln2)/(e) = 0.255fts^(-1)`

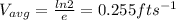
Explanation:

The question asks for the average velocity and not the instantaneous velocity (which would have meant to differentiate). So, the right formula is

`V_(avg) = (s(t_(2)) - s(t_(1) ) )/(t_(2) -t_(1) ) =`

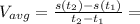
From the question,
`t_(1)` corresponds to e seconds and
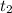`t_(2)` corresponds to 2e seconds. So, we have

`V_(avg) = (ln(2e) - ln(e))/(2e - e)`

One of the laws of logarithms says that

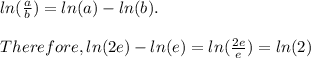
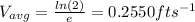`ln((a)/(b) )= ln(a) - ln(b). \\\\ Therefore, ln(2e) - ln(e) = ln((2e)/(e) ) = ln(2)`

`V_(avg) = (ln(2))/(e) = 0.2550fts^(-1)` ≅
`0.255fts^(-1)`