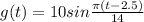Question

The power output, P, of a solar panel varies with the position of the sun. Let P = 10sinθ watts, where θ is the angle between the sun's rays and the panel, 0 ≤ θ ≤ π. On a typical summer day in Ann Arbor, Michigan, the sun rises at 6 am and sets at 8 pm and the angle is θ = πt/14, where t is time in hours since 6 am and 0 ≤ t ≤ 14. (a) Write a formula for a function, f(t), giving the power output of the solar panel (in watts) t hours after 6 am on a typical summer day in Ann Arbor. (b) Graph the function f(t) in part (a) for 0 ≤ t ≤ 14. (c) At what time is the power output greatest? What is the power output at this time? (d) On a typical winter day in Ann Arbor, the sun rises at 8 am and sets at 5 pm. Write a formula for a function, g(t), giving the power output of the solar panel (in watts) t hours after 8 am on a typical winter day.

Answer 1

Answers:

(a):

if θ = πt/14

and P = 10sinθ

then required function will be:

f(t) = 10sin(πt/14)

(b):

Graph for all 15 points i.e. t=0 (6 am) to t=14 (8 pm) is attached herewith this answer.

(c):

Power output will be maximum when sinθ=1

i.e.

πt/14=1

t=14/π OR t=4.4

Here 4 represents 10 am (as t=0 is 6 am) while 0.4 represents 24 minutes (0.4*60=24)

Hence, it will be maximum at 10:24 am and the value will be 10W because sinθ=1

(d):

If there is a delay of 2 hours in sun rise and 3 hours in sun set in winter season i.e. the power output which was at 6 am will now be at 8 am (2 hours delay in sun rise) and the power output which should be on 8 pm in summer will now be on 5 pm in winter (3 hours early sun set)then this delay will be compensated in time function i.e. πt/14. The average of these two values i.e. 2.5 will be subtracted from time

So, required function will be:

g(t) = 10sin{π(t-2.5)/14)}

`g(t) = 10sin(\pi(t-2.5) )/(14)`