Question

What is the vertex of the function f (x) = x2 - 10x?

(5,-25)
(5.-75)
(-5,75)
(-5,25)​

Answer 1

Option A

The vertex is (h, k) = (5, -25)

Solution:

Given function is:

`f(x) = x^2-10x`

The vertex form is given as:

`y = a(x-h)^2+k`

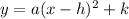
where (h, k) is the vertex

Rewrite the equation in vertex form

`f(x) = x^2-10x`

Complete the square for
`x^2-10x`

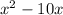
Use the form
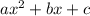`ax^2+bx+c` to find the values of a, b, c

a = 1 , b = -10, c = 0

Consider the vertex form of a parabola

`a(x+d)^2+e`

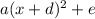
Substitute the values of a and b into the following formula to find "d" :

`d = (b)/(2a)\\\\d = (-10)/(2 * 1)\\\\d = -5`

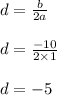
Find the value of "e" using the formula,

`e = c - (b^2)/(4a)\\\\e = 0 - ((-10)^2)/(4 * 1)\\\\e = -25`

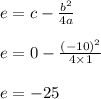
Substitute the value of a, d, e into vertex form

`a(x+d)^2+e\\\\1(x-5)^2-25\\\\(x-5)^2-25`

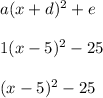
Set y equal to above equation

`y = (x-5)^2-25`

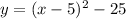
Compare the above equation with vertex form

`y = a(x-h)^2+k`

`y = (x-5)^2-25`

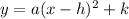
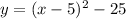
We find, h = 5 and k = -25

Thus the vertex is (h, k) = (5, -25)